이번 글에서 다룰 내용 이전 글에서 Priority Queue가 무엇인지, 내부가 어떻게 이루어져 있는지, 시간 복잡도는 어떻게 되는지 다루었다. 이번 글에서는 Kotlin에서 실제로 Priority Queue를 어떻게 선언하고 사용할 수 있는지 다루고자 한다. PriorityQueue 클래스 사용해 PriorityQueue 초기화하기 Kotlin에서 Priority Queue를 사용하기 위해서는 java.util 패키지의 PriorityQueue 클래스를 사용하면 된다. PriorityQueue 클래스는 다음과 같이 초기화할 수 있다. val priorityQueue = PriorityQueue() PriorityQueue에 값 삽입 하기 PriorityQueue에 값을 추가하기 위해서는 offer 함..
분류 전체보기
PriorityQueue란? PriorityQueue는 원소들을 우선순위에 따라 저장하고 관리하는 자료구조이다. 각각의 원소는 우선순위의 순서대로 저장된다. PriorityQueue는 일반적으로 min-heap 이나 max-heap을 사용해 구현된다. Heap은 트리 형태의 우선순위대로 순서가 나타내지는 자료 구조로. min-heap 방식으로 구현되면 우선순위가 낮은 요소가 맨 앞에 오고, 우선순위가 높은 요소가 맨 뒤에 오게 되며, max-heap 방식을 사용해 구현되면, 우선순위가 높은 요소가 맨 앞으로 오고 우선순위가 낮은 요소가 맨 뒤에 위치한다. Kotlin과 Java의 PriorityQueue는 min-heap 방식으로 구현되어 우선순위가 낮은 요소가 가장 앞쪽에 온다. 예를 들어 아래와 같이..
Binary Search Tree 구현하기 이전 글에서 Binary Search Tree가 무엇인지에 대해 살펴보았다. 이번 글에서는 이를 직접 구현해보려고 한다. 구현할 Binary Search Tree의 요구사항은 다음과 같다. 중복을 허용하지 않는다. 이미 있는 값의 추가 요청이 들어오면 아무런 동작을 하지 않고 반환한다. 노드는 임의로 다음과 같이 구성한다. data class Node(var value: Int) { var left: Node? = null var right: Node? = null } insert 메서드 구현하기 새로운 노드를 추가할 때는 다음과 같은 순서를 따른다. 추가 요청이 들어온 노드를 생성한다.(새로운 노드) 루트 노드가 null인지 확인 후 null이라면 새로운 노드..
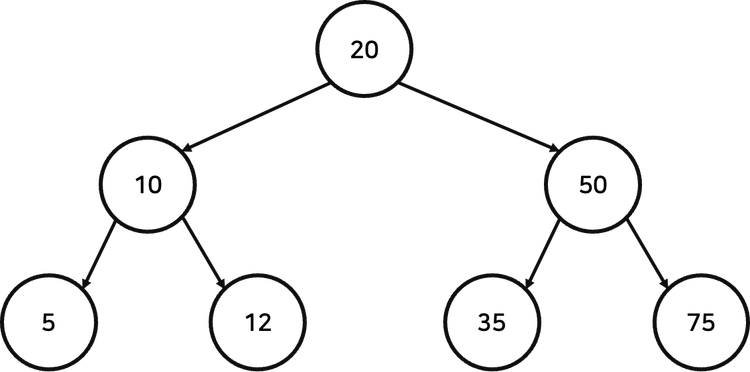
Binary Search Tree란? Binary Search Tree는 Binary Tree의 한 종류로써, 데이터를 저장하고 탐색하기 위한 자료 구조이다. Binary Search Tree는 각 노드가 특정한 값을 가지고 있고, 각 노드의 왼쪽 서브트리에는 노드의 값보다 더 작은 값의 노드들이, 오른쪽 서브트리에는 더 큰 값의 노드들이 위치하도록 만들어진다. 이러한 특성으로 인해 Binary Search Tree는 아래와 같은 특징을 가진다. 값들이 정렬되어 있는 Binary Tree 구조이다 : 특정 노드를 기준으로 해당 노드 왼쪽에 있는 노드들은 모두 해당 노드의 값보다 작은 값을 가지며, 해당 노드 오른쪽에 있는 노드들은 해당 노드의 값보다 큰 값을 가진다. 위와 같이 정렬되어 있어, Binar..
Kotlin에서 제곱 연산을 하는 방법 Kotlin에서 제곱 연산을 하려면 kotlin.math 패키지의 pow 연산을 쓰면 된다. pow연산은 Double, Float두가지 자료형에 대해 지원된다. Double 자료형 제곱 연산 Double 자료형은 Double이나 Int를 인자로 받아 제곱 연산(pow)을 수행할 수 있으며, 반환 자료형은 모두 Double이다. public actual inline fun Double.pow(x: Double): Double public actual inline fun Double.pow(n: Int): Double 예를 들어 아래와 같이 연산을 진행할 수 있다. println(2.0.pow(3.0)) // 8.0 출력 println(2.0.pow(3)) // 8.0..