삽입 정렬 알고리즘 이란 무엇인가?
삽입 정렬(Insertion Sort)은 배열의 각 원소를 해당 원소의 앞쪽에 있는 정렬된 배열의 적절한 위치에 삽입하는 방식으로 작동하는 배열이다. 각 원소가 삽입될 때 앞쪽 배열의 정렬된 위치에 들어가서 앞쪽 배열은 무조건 모두 정렬된 상태라는 것을 이용한 알고리즘이다.
예를 들어 아래와 같은 배열이 있을 때 둘째 원소부터 삽입 정렬을 수행한다고 하자.

둘째 원소는 첫 원소의 앞에 삽입된다.
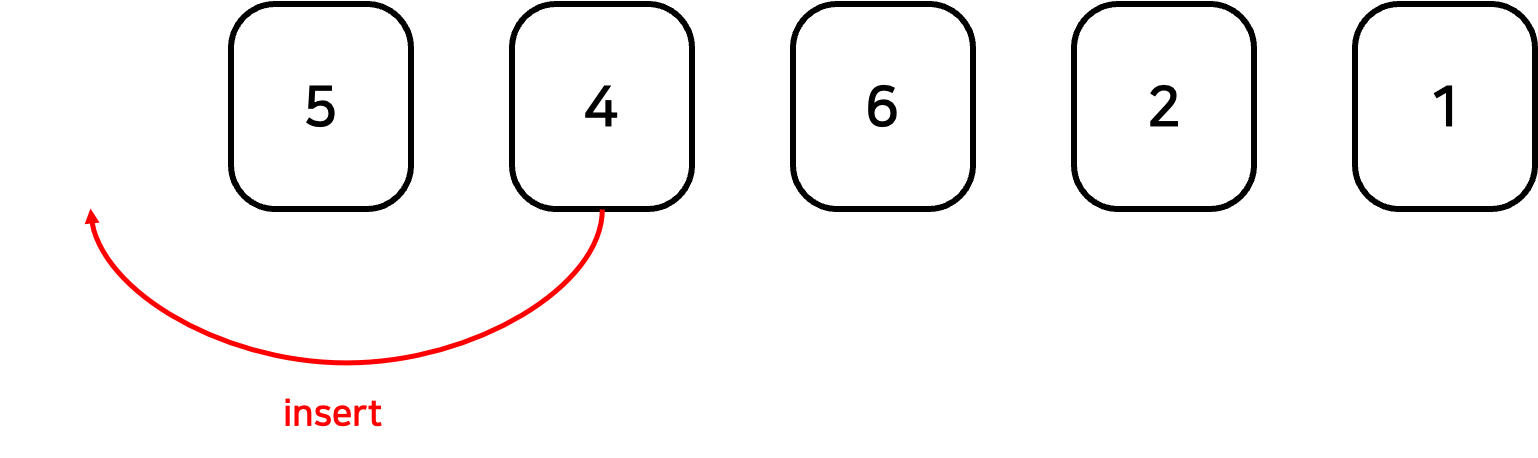
그러면 아래와 같은 형태의 배열이 나오고 포인터를 다음으로 이동시켰을 때 앞쪽 배열([4, 5])은 모두 정렬되어 있는 것을 볼 수 있다.
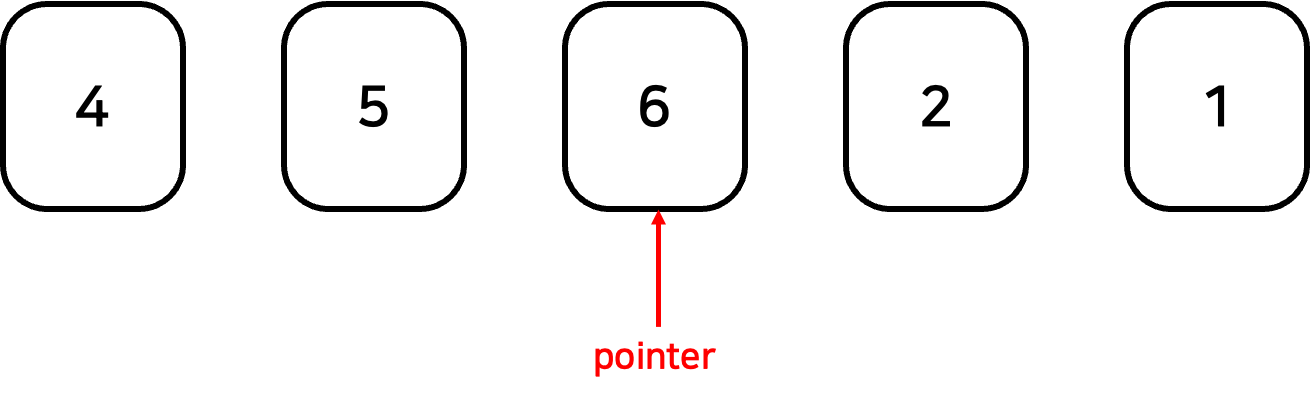
이를 남은 원소인 6, 2, 1에 대해서 마저 수행하면 정렬이 완료된다.
삽입 정렬에서 특정 값을 특정 위치에 삽입하기 위한 알고리즘
배열에 특정 값을 삽입하기 위해서는, 삽입해야 하는 위치의 모든 배열을 오른쪽으로 이동시킨 후 삽입 위치에 값을 삽입해야 한다.
1. 아래와 같이 구성된 배열이 있을 때, 2 노드를 맨 앞에 삽입하기 위해서는 4, 5, 6노드를 한 칸씩 이동해야 한다.

2. 따라서 2에 대한 값을 잃어버리면 안되므로 tmp변수에 저장해놓고 4, 5, 6을 오른쪽으로 한 칸씩 이동해야 한다.

3. 이후 저장된 2를 맨 앞에 삽입하면 된다.

삽입 정렬 메서드 구현하기
배열 오른쪽으로 한칸씩 이동하는 알고리즘 구현하기
삽입 정렬에는 배열을 오른쪽으로 한 칸씩 이동하는 것이 필요하기 때문에, 배열을 startIndex부터 finishIndex까지 오른쪽으로 한 칸씩 이동시키는 moveRight 메서드를 구현해야 한다.
fun moveRight(startIndex: Int, finishIndex: Int, array: IntArray) {
for (index in finishIndex downTo startIndex) {
array[index + 1] = array[index]
}
}
삽입 정렬 구현하기
삽입 정렬은 아래와 같은 순서로 구현될 수 있다.
1. 첫 원소는 무조건 해당 자리에서 변화가 없기 때문에 둘째 원소부터 시작해 마지막 원소까지 삽입을 수행하는 for문을 수행한다.
2. for문 내부에서는 해당 값이 어디에 삽입되어야 하는지 찾는 알고리즘을 만든다. childPointer은 현재 포인터의 바로 앞 노드(pointer-1 번) 부터 맨 앞 노드(0번) 노드까지 순환하면서 현재 값이 어디에 삽입되어야 하는지 위치를 찾는다.
3. 삽입 위치를 찾았으면, 삽입 되어야 하는 위치의 오른쪽에서부터 현재 위치의 왼쪽에 있는 모든 배열을 오른쪽으로 한 칸씩 이동한다.
4. 이후 삽입 위치에 현재 값을 넣는다.
5. 삽입이 되지 않았으면, 맨 앞이 위치라는 뜻이므로, 맨 앞 위치에 삽입을 수행한다.
fun insertionSort(array: IntArray) {
// 1. 둘째 노드부터 끝 노드까지 for문 수행
for (pointer in 1..array.size - 1) {
var currentValue = array[pointer]
var isInserted = false
// 2. 삽입 위치 탐색
for (childPointer in pointer - 1 downTo 0) {
// 현재 위치의 값이 childPointer 위치의 값보다 크다면, 현재 위치의 값이 childPointer 다음에 삽입 되어야 한다.
if (array[childPointer] < currentValue) {
// 3. 삽입 위치의 오른쪽, 현재 위치의 왼쪽에 있는 배열을 모두 오른쪽으로 한 칸씩 이동
moveRight(childPointer + 1, pointer - 1, array)
// 4. 삽입 위치에 현재 값 넣기
array[childPointer + 1] = currentValue
isInserted = true
break
}
}
// 5. 만약 현재 원소의 값이 모든 위치의 값보다 작다면 맨 앞에 삽입 되어야 한다.
// 따라서 맨 앞부터 현재 위치 전까지의 원소를 모두 오른쪽으로 한 칸씩 이동 후 맨 앞의 위치에 현재 원소를 삽입한다.
if (!isInserted) {
moveRight(0, pointer - 1, array)
array[0] = currentValue
}
}
}
만든 insertionSort 메서드를 수행해 보면 정상적으로 정렬이 수행되는 것을 확인할 수 있다.

삽입 정렬의 복잡도
시간 복잡도
삽입 정렬은 배열이 이미 정렬되어 있는 경우 삽입을 진행할 필요가 없어지므로, O(1)의 시간 복잡도로 정렬을 수행 가능하다.
하지만, 배열이 정렬되어 있지 않은 경우 평균적으로 O(N^2)의 시간 복잡도로 정렬을 수행한다.
공간 복잡도
추가적인 공간을 쓰지 않기 때문에 O(1)의 공간 복잡도를 가진다.

